PROBABILIDADES
Probabilidad. Concepto
Se define como el cálculo de probabilidad al conjunto de reglas que permiten determinar si un fenómeno ha de producirse, fundando la suposición en el cálculo, las estadísticas o la teoría.
EJERCICIO 1
Un banco local reporta que 80% de sus clientes tienen una cuenta de cheques, 60% una cuenta de ahorros, y 50% tienen ambas. Si se selecciona un cliente al azar:

a. ¿Cuál es la probabilidad de que este tenga una cuenta corriente o una de ahorros?

b. ¿Cuál es la probabilidad de que el cliente no tenga ninguna de las dos?
1 - 0,90 = 0,10
EJERCICIO 2
La Asociación de Comidas Típicas pusieron un anuncio en el diario El Comercio, y ellos estiman que el 1% de los suscriptores se acercarán a la feria a probarsus platos. Asimismo, consideran que 0,5% de los no suscriptores tambiénse acercarán a la feria, y que existe 1 posibilidad en 20 de que una persona sea un suscriptor.
a. Encuentre la probabilidad de que una persona seleccionada al azar asistirá a la feria

b. Si una persona asiste a la feria, ¿cuál es la probabilidad de que sea un suscriptor del diario?

c. Si una persona no asiste a la feria, ¿cuál es la probabilidad de que sea un suscriptor del diario?

EJERCICIO 3
El comisariato de la policia de Wood County clasifica los delitos de acuerdo con la edad ( en años) del malhechor, y si el crimen ocurrió con violencia o sin ella. Como se muestra a continuación, al comisario le reportaron un total de 150 delitos cometidos durante el pasado año.
| T. delito | menos 20 | 20 a 40 | 40 o más | Total |
| Con violencia | 27 | 41 | 14 | 82 |
| Sin violencia | 12 | 34 | 22 | 68 |
| Total | 39 | 75 | 36 | 150 |
a. Cuál es la probabilidad de seleccionar un caso para analizarlo y encontrar que fue un delito con violencia?
P(A) = 82 / 150 = 0,546
b. Cuál es la probabilidad de seleccionar un caso para analizarlo y descubrir que el delito lo cometió alguién con menos de 40 años de edad?
P(A o B) = P(A ) + P(B)
P(A o B) = ( 39 / 150 ) + ( 75 / 150 )
P(A o B) = 0,26 + 0,50
P(A o B) = 0,76
c. Cuál es la probabilidad de seleccionar un caso y que el crimen haya sido cometido con violencia o que el delincuente tenga menos de 20 años? Qué regla de adición se aplicó?
P(A o B) = P(A ) + P(B) - P( A y B )
P(A o B) = 82 / 150 + 39 / 150 - 27 / 150
P(A o B) = 0,546 + 0,26 - 0,18
P(A o B) = 0,626
Se aplicó la regla general de la adición.
d. dado que se seleciona para análisis un delito con violencia, cuál es la probabilidad de que lo haya cometido una persona menor de 20 años?
P ( A1 ) = 27 / 82 = 0,329
e. Un juez seleccionó dos casos para revisarlos. Cuál es la probabilidad de que ambos sean crímenes cometidos con violencia?
P ( A y B ) = P (A ) P ( B )
P ( A y B ) = ( 82 / 150 ) ( 81 / 149 )
P ( A y B ) = ( 0,546 )( 0,543 )
P ( A y B ) = 0,296
EJERCICIO 4
Si tenemos en una caja 15 piedras verdes y 9 piedras rojas. La probabilidad de sacar una piedra roja en un intento es:

EJERCICIO 5
Supongamos que se extrae una carta de una baraja de 52 cartas bien barajada. ¿Cuál es la probabilidad de que la carta sea o un rey o una figura negra? (Evento no mutuamente excluyente)
Hay 52 sucesos o eventos simples. Sean los sucesos o eventos
Hay 4 reyes. A = Que la carta sea un rey.
Hay 6 figuras negras B = Que la carta sea una figura negra
P ( A U B ) =P( A ) + P( B ) – P( A ∩ B )
P(A U B)= 4/52 + 6/52 – 2/52 = 8/52= 0.15
EJERCICIO 6
Cuál es la probabilidad de obtener un total de 7 u 11 cuando se lanza un par de dados?
s(7)={ (1,6),(2,5),(3,4),(6,1),(5,2),(4,3) }
s(11)={ (5,6),(6,5) }
P(7)= 6/36 = 1/6
P(11)= 2/36
EJERCICIO 7
Sean A y B dos sucesos aleatorios con p(A) = 1/2, p(B) = 1/3, p(A B)= 1/4. Determinar:

EJERCICIO 8
Hallar la probabilidad de que al lanzar al aire dos monedas, salgan:
1. Dos caras
2. Dos cruces
3. Dos caras y una cruz
Solución: Diagrama de árbol


EJERCICIO 9
Hallar la probabilidad de que al levantar unas fichas de dominó se obtenga un número de puntos mayor que 9 o que sea múltiplo de 4.

EJERCICIO 10
Un dado está trucado, de forma que las probabilidades de obtener las distintas caras son proporcionales a los números de estas.
Hallar:
1. La probabilidad de obtener el 6 en un lanzamiento.
2. La probabilidad de conseguir un número impar en un lanzamiento
Solución:

EJERCICIO 11
Se lanzan dos dados al aire y se anota la suma de los puntos obtenidos. Se pide:
1. La probabilidad de que salga el 7.
2. La probabilidad de que el número obtenido sea par.
3. La probabilidad de que el número obtenido sea múltiplo de tres.
Solución:

EJERCICIO 12
Se lanzan tres dados. Encontrar la probabilidad de que:
1. Salga 6 en todos
2. Los puntos obtenidos sumen 7
Solución:

EJERCICIO 13
Buscar la probabilidad de que al echar un dado al aire, salga:
1. Un número par
2. Un múltiplo de 3
3. Mayor que 4
Solución:

EJERCICIO 14
Se sacan dos bolas de una urna que se compone de una bola blanca, otra roja, otra verde y otra negra. Describir el espacio muestral cuando:
1.La primera bola se devuelve a la urna antes de sacar la segunda.
2. La primera bola no se devuelve
Solución:

EJERCICIO 15
Una urna tiene ocho bolas rojas, 5 amarilla y siete verdes. Se extrae una al azar de que:
1. Sea roja
2. Sea verde
3. Sea amarilla
4. No sea roja
5. No sea amarilla
Solución:

PROBABILIDADES
Concepto:
Es el conjunto de reglas que permiten determinar si un fenómeno ha de producirse, luego de un experimento aleatorio y condiciones estables.
RESOLUCION DE EJERCICIOS: MAYOR INFORMACION Whatsapp 0984347752
1. A una reunión asisten 10 personas y se intercambian saludos entre todos.
¿Cuántos saludos se han intercambiado?
P(2)= (10 * 9)/2 =45
2. Tablas de contingencia
|
|
EMPLEADO |
DESEMPLEADO |
TOTAL |
|
HOMBRE |
460 |
40 |
500 |
|
MUJER |
140 |
260 |
400 |
|
TOTAL |
600 |
300 |
900 |
Cuál es la probabilidad total de hombre?
- P(h)= 600/900*460/600 +300/900*40/300= 25/45
-
Se elige una persona al azar cuál es la probabilidad que la persona elegida sea hombre y que tenga empleo?
Teorema de Bayes:
P(H/E)= P(H∩E)/P(E)
P= P(H∩E) = 460/900
P(E)= 600/900
P(H/E)= 460/900 / 600/900 = 23/30 Probabilidad de H dado E
Aprendizaje % por % práctico, mediante ejercicios de probabilidades con casos de la vida real y ajustados a la carrera de estudio.
Capacítate en probabilidades Estadísticas con Ingenieros Estadísticos
Tf: 0997 314271
WHATSAPP: 0984 347752
DISTRIBUCIÓN DE PROBABILIDAD
DE POISSON
Ejercicio 1
La señora Bergen está encargada de los préstamos en el banco Coast Bank and Trust. Con base en sus años de experiencia, estima que la probabilidad de que un solicitante no sea capaz de pagar su préstamo,
es 0.025. El mes pasado realizó 40 préstamos.
DATOS:

1. ¿Cuál es la probabilidad de que 3 préstamos no sean pagados a tiempo?

2. ¿Y cuál es la de que por lo menos 3 préstamos no se liquiden a tiempo?

Ejercicio 2
Se estima que 0.5% de las llamadas telefónicas al departamento de facturación de la U.S. las 1200
llamadas del día de hoy, por lo menos 5 hayan recibido dicha señal?

Ejercicio 3
Un fabricante de marcos para ventana sabe por experiencia que 5% de la producción
tendrá algún tipo de defecto menor, el cual requerirá un ligero arreglo. ¿Cuál es la probabilidad de que en una muestra de 20 marcos:
DATOS:

1. Ninguno necesite arreglo?

2. Por lo menos 1 requerirá tal ajuste?

3. Más de 2 necesitaran arreglo?

Ejercicio 4
En el último reporte de la Policía Judicial se evidenció que existe 3,1 robos por minuto. Supóngase que la
distribución de los robos por minuto se puede aproximar por medio de una distribución de probabilidad de Poisson.
DATOS:

1. Calcule la probabilidad de que ocurran exactamente cuatro robos en un minuto.

2. ¿Cuál es la probabilidad de que no haya ningún robo en un minuto?

3. ¿Cuál es la probabilidad de que haya por lo menos un robo en un minuto?

Ejercicios: Suma, Multiplicación y Complemento de probabilidades
EJERCICIO 1
La probabilidad de que un avión bombardero acierte en su objetivo en una misión es 0,80. Se envían cuatro bombarderos hacia el mismo objetivo. Cuál es la probabilidad de que:
a) Todos den en el blanco?

b) Ninguno acierte el objetivo?
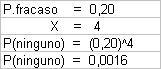
c) Al menos uno acierte en el blanco?
P(al menos uno) = 1 - 0,0016
P(al menos uno) = 0,9984
EJERCICIO 2
Hay 100 empleados en la empresa Kiddie Carts International, de esos 57 son de producción, 40 son supervisores, 2 son secretarias y el empleado restante es el director general. Suponga que se selecciona un empleado de ese grupo:
a) Cuál es la probabilidad de que la persona elegida labore en producción?
P(1 labore producción) = 57 / 100
P(1 labore producción) = 0,57
b) Cuál es la probabilidad de que el empleado seleccionado sea de producción o un supervisor?

c) Son los eventos del inciso (b) mutuamente excluyentes?
Los eventos del inciso (b) si son mutuamente excluyentes, ya que el empleado no puede ser de producción y supervisor al mismo tiempo.
d) Cuál es la probabilidad de que el empleado elegido no sea de producción ni un supervisor?
P ( no producc. ni supervisor) = 1 - 0,97
P ( no producc. ni supervisor) = 0,03
EJERCICIO 3
La empresa Flashner arketing Research se especializa en proporcionar evaluaciones de sus perpectivas a toiendas de ropa para dama en centros comerciales. Albert Flashner el director informa que evalúa las posibilkidades como buenas, regulares o malas. Los registros de las evaluaciones anteriores indican que en 60% de los casos, las perpectivas son buenas , en 30% las perpectivas son regulares y en 10% son malas . De las evaluadas como buena, 80% dieron utilidades durante el primer año y de las evaluadas como regulare, 60% produjeron utilidades el primer año y de las clasificadas como malas 20% arrojaron beneficios durante el primer año. Connies Apparel fue uno de los clientes de Flashner que obtuvo utilidades el año pasado. Cuál es la probabilidad de que se le haya dado una clasificación inicial de mala?

